3 Kopiering - att skapa många formler
Exempel 3.1
Autofyll
Gör ett
kalkylark med vilket man kan bilda de 10 på varandra föl-jande heltalen a, a
+ 1, a + 2 ... a + 9, för olika heltal, a.
Vi börjar med att bilda talen 1, 2, 3 … 10. Vi
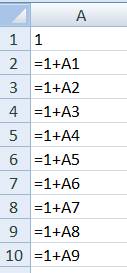
1. Skriv in 1
i cell A1.
Vi kan göra detta genom att se till att dessa formler
hamnar i cellerna A3, A4, … ,A10.
Detta går att göra på ett mycket bekvämt sätt.
2. Skriv in formeln =1+A1 i cell A2.
Resten av formlerna får vi på plats på följande
sätt.
3. Placera cellmarkören i cell A2,
b) flytta muspekaren till den
lilla svarta kvadraten i nedre högra hörnet av cellen
c) när muspekaren blivit
ett kors, skall vänster musknapp tryckas ned och musen dras nedåt så att området A2 : A10 blir markerat. När vänster
musknapp släpps är saken klar.
Genom att flytta
cellmarkören till cellerna A1, A2 ...... A10, kan man i formelraden se
vilka formler, som finns i de olika cellerna. Man ser att det blev som vi ville. Formeln =1+A2
ligger i cell A3, =1+A3 i cell A4 osv.
Kopiering
Vi har kopierat innehållet i A2, formeln =1+A1,
nedåt. Vi använde oss av hjälpmedlet Autofyll.
Matematisk kommentar
Vi har bildat de 10
första talen i den rekursiva talföljden
{
a
0
=1
a
n+1
=1+
a
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabeqaaiaadggadaWgaaWcbaGaaGimaaqabaGccqGH9aqpcaaIXaaabaGaamyyamaaBaaaleaacaWGUbGaey4kaSIaaGymaaqabaGccqGH9aqpcaaIXaGaey4kaSIaamyyamaaBaaaleaacaWGUbaabeaaaaGccaGL7baaaaa@42FB@
Genom att skriva in olika
heltal i cell A1 kan man få andra följder med 10 på varandra följande heltal.
Exempel 3.2
Absoluta och relativa cellreferenser
Gör ett kalkylblad med
vilket man kan bilda
n
a
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBamaaCaaaleqabaGaamyyaaaaaaa@37EA@
,
(n+1)
a
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaad6gacqGHRaWkcaaIXaGaaiykamaaCaaaleqabaGaamyyaaaaaaa@3AE0@
,
(n+2)
a
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaad6gacqGHRaWkcaaIYaGaaiykamaaCaaaleqabaGaamyyaaaaaaa@3AE1@
,
(n+3)
a
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeWaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaad6gacqGHRaWkcaaIZaGaaiykamaaCaaaleqabaGaamyyaaaaaaa@3AE3@
och
(n+4)
a
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaad6gacqGHRaWkcaaI0aGaaiykamaaCaaaleqabaGaamyyaaaaaaa@3AE3@
för olika
värden på n och a.
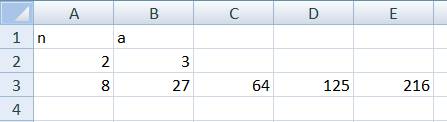
Om n = 2 och a = 3 bör vi få
ett sådant här resultat.
1. Skriv in n
i cell A1 och a i cell B1.
2. Skriv in 3
i cell B2.
3. Skriv in 2
cell A2.
4. Skriv in formeln =A2 i cell A3.
5. Lägg in formeln =1+A3 i cell B3.
6. Markera B3 och kopiera innehållet i B3 till
området B3 : E3 med Autofyll.
7. Lägg in formeln =A3^$B2 i cell A4.
8. Kopiera innehållet i cell A4 till området B4 : E4.
(Studera formlerna i området A4 : E4. Undersök
betydelsen av $-tecknet. Vad händer om man utelämnar $-tecknet i 7?)
Området A4 : E4 innehåller de sökta talen för n = 2 och a = 3.
Genom att ändra innehållet i cellerna A2 och B2
kan man ändra värdet av n och a.
n = 3 och a
= 5 ger talen 243, 1024, 3125, 7776 och 16807
Exempel 3.3
Absoluta och relativa cellreferenser igen
Gör ett
kalkylblad med vilket man kan beräkna
x
2
+a
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaadggaaaa@399C@
, där x = 1, 2, 3 ... , 20 för olika värden på
a .
1. Skriv in x,
x^2 + a och a i cellerna A1, B1 resp. C1.
2. Skriv in 1
i cell A2.
3. Lägg in formeln =1+A2 i cell A3.
4. Lägg in formeln =A2^2+C$2 i cell B2.
5. Kopiera innehållet i cell B2 till cell B3 genom
att
a) placera
cellmarkören i cell B2,
b) flytta
muspekaren till den lilla svarta
kvadraten i nedre högra hörnet av cellen
c) när muspekaren blivit ett kors, skall
vänster musknapp tryckas ned och musen dras nedåt så att området B2 : B3 blir markerat. När vänster
musknapp släpps är kopieringen utförd.
6. Placera cellmarkören i cell A3 samt markera
området A3 : B21.
7. Ge kommandot Redigera
Fyll Ned.
Området B2 : B21 innehåller nu kvadraterna på de
20 första heltalen.
Eftersom cell C2 är tom är värdet på a = 0. Genom att lägga in olika tal i
cell C2 kan värdet på a varieras.
Studera formlerna i området B2 : B21. Undersök
betydelsen av $-tecknet.
Exempel 3.4 Absoluta och relativa
cellreferenser ytterligare en gång samt hantering av valutor och antalet
decimaler
Vi skall beräkna till
vilket belopp ett kapital, K kr,
växer efter en viss tid, n år, med en viss räntesats, p %.
Behållningen efter n
år ges av formeln
K
(
1+
p
100
)
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8sipiYdHaVhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGlbWaaeWaaeaacaaIXaGaey4kaSYaaSaaaeaacaWGWbaabaGaaGymaiaaicdacaaIWaaaaaGaayjkaiaawMcaamaaCaaaleqabaGaamOBaaaaaaa@3CE6@
Gör ett kalkylblad med
vilket man samtidigt kan beräkna behållningen av kapitalen K kr, (K
+ a) kr, (K + 2a) kr, (K + 3a) kr, (K
+ 4a) kr samt (K + 5a) kr efter n år, (n + b)
år, (n + 2b) år, (n + 3b) år, (n + 4b)
år samt (n + 5b) år. Värdet av K, p, a, b
och n skall kunna varieras.
Om K = 1000, a = 500, b
= 5, n = 5 och p = 4,5 får man detta resultat.
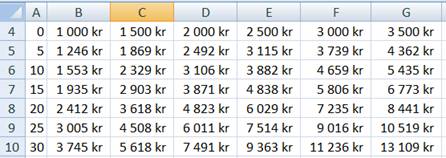
1. Skriv in text
och variabelvärden i området A1:G3 enligt figuren ovan.
2. Skriv in
formlerna =F2 i
cell A4 och =A4
+E$2 i cell A6 samt kopiera nedåt till cell A10.
3. Skriv in
formlerna =C2 i
B4 och =B4+$D2 i C4 samt kopiera åt höger till cell G4.
4. Skriv in formeln =B$4*(1+$B$2/100)^$A5 i cell
B5 samt fyll åt höger till cell G5 samt sedan neråt till cell G10.
Man kan ge ett område
formatet Valuta genom att först markera det och sedan klicka på ikonen Valuta,  . Man kan minska antalet decimaler med ikonen Minska decimal,
. Man kan minska antalet decimaler med ikonen Minska decimal,  .
.
Exempel 3.5 Ett närmevärde
Vi skall använda en
metod, som härrör från C. F. Gauss för att approximera, d.v.s. bestämma ett
närmevärde till, p.
Definiera talföljderna
a
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaaaaa@37E9@
,
b
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOyamaaBaaaleaacaWGUbaabeaaaaa@37EA@
,
c
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4yamaaBaaaleaacaWGUbaabeaaaaa@37EB@
och
x
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGUbaabeaaaaa@3800@
på följande sätt.
a
1
=1
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaaIXaaabeaakiabg2da9iaaigdaaaa@397C@
,
b
1
=
1
2
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOyamaaBaaaleaacaaIXaaabeaakiabg2da9maalaaabaGaaGymaaqaamaakaaabaGaaGOmaaWcbeaaaaaaaa@3A64@
,
c
1
=
1
4
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4yamaaBaaaleaacaaIXaaabeaakiabg2da9maalaaabaGaaGymaaqaaiaaisdaaaaaaa@3A4C@
och
x
1
=1
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaaIXaaabeaakiabg2da9iaaigdaaaa@3993@
a
n+1
=
a
n
+
b
n
2
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbGaey4kaSIaaGymaaqabaGccqGH9aqpdaWcaaqaaiaadggadaWgaaWcbaGaamOBaaqabaGccqGHRaWkcaWGIbWaaSbaaSqaaiaad6gaaeqaaaGcbaGaaGOmaaaaaaa@4063@
b
n+1
=
b
n
a
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOyamaaBaaaleaacaWGUbGaey4kaSIaaGymaaqabaGccqGH9aqpdaGcaaqaaiaadkgadaWgaaWcbaGaamOBaaqabaGccaWGHbWaaSbaaSqaaiaad6gaaeqaaaqabaaaaa@3EBC@
c
n+1
=
c
n
−
x
n
(
a
n+1
−
a
n
)
2
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4yamaaBaaaleaacaWGUbGaey4kaSIaaGymaaqabaGccqGH9aqpcaWGJbWaaSbaaSqaaiaad6gaaeqaaOGaeyOeI0IaamiEamaaBaaaleaacaWGUbaabeaakiaacIcacaWGHbWaaSbaaSqaaiaad6gacqGHRaWkcaaIXaaabeaakiabgkHiTiaadggadaWgaaWcbaGaamOBaaqabaGccaGGPaWaaWbaaSqabeaacaaIYaaaaaaa@48A6@
x
n+1
=2
x
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaWGUbGaey4kaSIaaGymaaqabaGccqGH9aqpcaaIYaGaamiEamaaBaaaleaacaWGUbaabeaaaaa@3D85@
y
n
=
(
a
n+1
+
b
n+1
)
2
4
c
n+1
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaWGUbaabeaakiabg2da9maalaaabaGaaiikaiaadggadaWgaaWcbaGaamOBaiabgUcaRiaaigdaaeqaaOGaey4kaSIaamOyamaaBaaaleaacaWGUbGaey4kaSIaaGymaaqabaGccaGGPaWaaWbaaSqabeaacaaIYaaaaaGcbaGaaGinaiaadogadaWgaaWcbaGaamOBaiabgUcaRiaaigdaaeqaaaaaaaa@480A@
Gör ett kalkylblad med
vilket du kan beräkna
y
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaWGUbaabeaaaaa@3801@
, n = 1, 2 ... 7 och visa numeriskt att
lim
n→∞
y
n
=π
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaCbeaeaaciGGSbGaaiyAaiaac2gaaSqaaiaad6gacqGHsgIRcqGHEisPaeqaaOGaamyEamaaBaaaleaacaWGUbaabeaakiabg2da9iabec8aWbaa@4232@
.
1. Skriv in a, b,
c, x och y i cellerna A1,
B1, C1, D1 och E1.
2. Skriv in 1, =1/ROT(2), =1/4 och 1 into the cells A2, B2, C2 och D2.
3. Skriv in formlerna =(A2+B2)/2, =ROT(B2*A2),
=C2-D2*(A3-A2)^2, =2*D2 och =(A3+B3)^2/(4*C3) I cellerna A3, B3, C3, D3 och E3.
Du bör nu ha detta
kalkylblad.

Figur 3.1
4. Kopiera formlerna i området
A3 : E3 till området A4 : E9.
5. Man finner nu värdena
på
y
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaWGUbaabeaaaaa@3801@
, n = 1, 2, ... 7 i
området E3 : E9.
6. Alla värden i ett kalkylblad
lagras med 15 siffrors noggrannhet. I detta exempel kan det vara av intresse
att se alla 15 siffrorna I området E3 : E9.
a) Markera området E3 :
E9.
b) Högerklicka och välj
sedan Formatera celleroch gör val
enligt dialogrutan nedan.
Figur 3.2
Vi ser att
y
1
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaaIXaaabeaaaaa@37C9@
= 3.14057925052217,
y
2
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaaIYaaabeaaaaa@37CA@
=
3.14159264621354 och
y
i
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaWGPbaabeaaaaa@37FC@
= 3.14159265358979 for i = 3, 4, 5, 6 och 7.
7. Man kan få ett
närmevärde till p med 15 korrekta siffror genom att skriva in formuleln
=PI() I en cell och göra som ovan.
Vi kan nu dra slutsatsen
att
y
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaWGUbaabeaaaaa@3801@
tycks konvergera mot p mycket snabbt. Man har visat att antalet korrekta siffror ökar så snabbt
att att till exempel
y
19
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEamaaBaaaleaacaaIXaGaaGyoaaqabaaaaa@388C@
ger ett närmevärde till p med cirka 1 000 000 korrekta siffror.
Exempel 3.6 Aritmetiska talföljder
En talföljd
a
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaaaaa@37E9@
, n = 1,
2, 3 … kallas aritmetisk om
skillnaden mellan ett tal och det föregående alltid har samma värde, d. Det betyder att
a
k
=
a
k−1
+d
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGRbaabeaakiabg2da9iaadggadaWgaaWcbaGaam4AaiabgkHiTiaaigdaaeqaaOGaey4kaSIaamizaaaa@3E75@
, k = 2, 3, 4 … (1)
d
kallas den aritmetiska talföljdens differens.
Låt
S
n
=
a
1
+
a
2
+ ... +
a
n
=
∑
k=1
n
a
k
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaakiabg2da9iaadggadaWgaaWcbaGaaGymaaqabaGccqGHRaWkcaWGHbWaaSbaaSqaaiaaikdaaeqaaOGaaGjbVlabgUcaRiaaysW7caGGUaGaaiOlaiaac6cacaaMe8UaaGjbVlabgUcaRiaadggadaWgaaWcbaGaamOBaaqabaGccqGH9aqpdaaeWbqaaiaadggadaWgaaWcbaGaam4AaaqabaaabaGaam4Aaiabg2da9iaaigdaaeaacaWGUbaaniabggHiLdaaaa@527C@
summan av
de n första termerna i den aritmetiska
talföljden
a
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaaaaa@37E9@
. Följande formel är välkänd
S
n
=n
a
1
+
a
n
2
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaakiabg2da9iaad6gadaWcaaqaaiaadggadaWgaaWcbaGaaGymaaqabaGccqGHRaWkcaWGHbWaaSbaaSqaaiaad6gaaeqaaaGcbaGaaGOmaaaaaaa@3F72@
(2)
Man kan tolka denna
formel på följnde sätt.
Summan av en aritmetisk
talföljd är lika med antalet termer multiplicerat med medelvärdet av summans
första och sista term.
Gör ett kalkylblad med vilket du kan generera de
10 första termerna I en aritmetisk talföljd med given första term och given
differens samt bekräfta att formeln
S
n
=n
a
1
+
a
n
2
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaakiabg2da9iaad6gadaWcaaqaaiaadggadaWgaaWcbaGaaGymaaqabaGccqGHRaWkcaWGHbWaaSbaaSqaaiaad6gaaeqaaaGcbaGaaGOmaaaaaaa@3F72@
är korrekt för n = 1, 2, 3 ... 10.
1. Skriv in termer, Sn, SUMMA, första_term och differens i cellerna A1, B1, C1, D1 och E1
2. Skriv in 1 och 2 i cellerna D2 och E2.
3. Definiera variablerna första_term och differens genom att markera området D1 : E2 och trycka
CTRL+SHIFT+F3.
4. Skriv in formeln = första_term i cell A2.
5. Skriv in formeln =A2+differens
i cellA3.
6. Kopiera formeln i cell
A3 till området A4 : A11.
Vi skall nu använda
kalkylbladsfunktionerna ANTAL, MEDEL och SUMMA. ANTAL ger antalet tal i ett
område. MEDEL ger medelvärdet av alla tal i ett område. SUMMA ger summan av
alla tal i ett område.
7. Skriv in formeln =ANTAL(A$2:A2)*MEDEL(första_term;A2) i
cell B2 samt kopiera till B3:B11.
Vi skall nu på två olika
sätt direkt beräkna
S
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaaaaa@37DB@
för n
= 1, 2, 3 … 10
8. Skriv in formeln =SUMMMA(A$2:A2) i cell C2 samt kopiera
till C3:C11.
9. Skriv in formeln = första_term i cell D2 samt formeln =D2+A3 i cell D3.
Koiera till D4 : D11.
Vi har nu
n
a
1
+
a
n
2
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOBamaalaaabaGaamyyamaaBaaaleaacaaIXaaabeaakiabgUcaRiaadggadaWgaaWcbaGaamOBaaqabaaakeaacaaIYaaaaaaa@3C6B@
för n =
1, 2 ... 10 i kolumn B samt
S
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaaaaa@37DB@
för n = 1, 2 ... 10 i kolumnerna C och D. Vi
ser att formeln
S
n
=n
a
1
+
a
n
2
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaakiabg2da9iaad6gadaWcaaqaaiaadggadaWgaaWcbaGaaGymaaqabaGccqGHRaWkcaWGHbWaaSbaaSqaaiaad6gaaeqaaaGcbaGaaGOmaaaaaaa@3F72@
stämmer om första termen är 1 och differensen är 2. Om vi varierar värdet
av första termen och på differensen att den fortfarande stämmer.
Övningsuppgifter
1. Gör ett kalkylblad med vilket man kan bilda 10 på
varandra följande jämna talen 2k, 2k + 2, 2k + 4, ...... 2k + 18 i
området A1 : A10 för olika heltal k.
2. Gör ett kalkylblad med vilket man kan bilda 10 på
varandra udda tal 2k + 1, 2k + 3, ... 2k + 19 i området B1 : K1, för olika heltal k.
3. Den s.k. Fibonacciföljden definieras
på följande sätt.
a0 = 0 , a1 = 1, an+2 = an+1 + an d.v.s. de två första talen är 0 och 1, sedan
får man varje tal genom att bilda summan av de två föregående.
a) Gör ett kalkylblad med vilket man kan beräkna
a
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaaaaa@37EA@
för n = 0, 1 ..... 53.
b) Beräkna a53.
Fibonacciföljden är här given i s.k. rekursiv form.
Man kan beräkna
a
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaaaaa@37EA@
i sluten
form genom att med hjälp av teorin för linjära differensekvationer visa att
a
n
=
1
5
(
1+
5
2
)
n
−
1
5
(
1−
5
2
)
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaakiabg2da9maalaaabaGaaGymaaqaamaakaaabaGaaGynaaWcbeaaaaGcdaqadaqaamaalaaabaGaaGymaiabgUcaRmaakaaabaGaaGynaaWcbeaaaOqaaiaaikdaaaaacaGLOaGaayzkaaWaaWbaaSqabeaacaWGUbaaaOGaeyOeI0YaaSaaaeaacaaIXaaabaWaaOaaaeaacaaI1aaaleqaaaaakmaabmaabaWaaSaaaeaacaaIXaGaeyOeI0YaaOaaaeaacaaI1aaaleqaaaGcbaGaaGOmaaaaaiaawIcacaGLPaaadaahaaWcbeqaaiaad6gaaaaaaa@4946@
c) Beräkna
a53 om a1 = 1, a2 = 2.
4. Gör ett kalkylblad med vilket man kan beräkna
behållningen efter 5, 10, 15 och 20 år av ett år 0 insatt kapital på 1000 kr,
15 000 kr 25 000 kr och 30 000 kr. Räntesatsen skall kunna varieras.
5. 1000 kr sätts in på ett bankkonto med räntesatsen
5 % i början av år 2002. Beräkna behållningen på kontot under vart och ett av
de följande 10 åren om räntesatsen varje år
a) minskar med 0,1 procentenhet.
b) ökar med 0,1 procentenhet.
6. En
person sätter in pengar på ett konto enligt tabellen nedan.
|
år
|
räntesats
under året
|
insättning i början av året
|
|
0
|
3
|
1 234 kr
|
|
1
|
3,4
|
345 kr
|
|
2
|
2,1
|
789 kr
|
|
3
|
4,2
|
1 287 kr
|
|
4
|
3,5
|
765 kr
|
|
5
|
3,7
|
4 321 kr
|
|
6
|
2,8
|
5 671 kr
|
|
7
|
2,7
|
9 753 kr
|
|
8
|
3,8
|
1 479 kr
|
|
9
|
5
|
1 298 kr
|
a)
Beräkna behållningen i början av vart och ett av år 0, 1, 2 … 9.
b)
Beräkna den genomsnittsliga räntesatsen under10-årsperioden.
7. Gör ett kalkylblad med vilket man kan beräkna
f
′
(a)
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafaGaaiikaiaadggacaGGPaaaaa@391A@
numeriskt
för olika värden på a, om f(x)
=
a)
e
x
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyzamaaCaaaleqabaGaamiEaaaaaaa@37F8@
(skrivs
=exp(x) i Excel) b)
sinx
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaci4CaiaacMgacaGGUbGaamiEaaaa@39B9@
c)
lnx
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6gacaWG4baaaa@38C5@
d)
x
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaOaaaeaacaWG4baaleqaaaaa@36FC@
e)
x
b
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaCaaaleqabaGaamOyaaaaaaa@37F5@
, där a och
b kan anta olika värden.
Använd derivatans
definition d.v.s.
f
′
(
a
)=
lim
h→0
f(
a+h
)−f(
a
)
h
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafaWaaeWaaeaacaWGHbaacaGLOaGaayzkaaGaeyypa0ZaaCbeaeaaciGGSbGaaiyAaiaac2gaaSqaaiaadIgacqGHsgIRcaaIWaaabeaakmaalaaabaGaamOzamaabmaabaGaamyyaiabgUcaRiaadIgaaiaawIcacaGLPaaacqGHsislcaWGMbWaaeWaaeaacaWGHbaacaGLOaGaayzkaaaabaGaamiAaaaaaaa@4B65@
.
Beräkna
f(
a+h
)−f(
a
)
h
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWGMbWaaeWaaeaacaWGHbGaey4kaSIaamiAaaGaayjkaiaawMcaaiabgkHiTiaadAgadaqadaqaaiaadggaaiaawIcacaGLPaaaaeaacaWGObaaaaaa@4052@
för h = 1; 0,1; 0,01; … 10-9.
Vad händer om man
väljer ett ännu mindre värde på h,
exempelvis
h=
10
−14
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiAaiabg2da9iaaigdacaaIWaWaaWbaaSqabeaacqGHsislcaaIXaGaaGinaaaaaaa@3BE0@
?
8.
Gör ett kalkylblad med vars hjälp man kan bilda talföljden
a
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaaaaa@37E9@
, där
a
n
={
2n, om n är udda
3n, om n är
jämnt
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaakiabg2da9maaceaaeaqabeaacaaIYaGaamOBaiaacYcacaaMe8Uaae4Baiaab2gacaaMe8UaamOBaiaaysW7caqGKdGaaeOCaiabl2==UjaabwhacaqGKbGaaeizaiaabggaaeaacaaIZaGaamOBaiaacYcacaaMe8Uaae4Baiaab2gacaaMe8UaamOBaiaaysW7caqGKdGaaeOCaiabl2==UjaabQgacaqGKdGaaeyBaiaab6gacaqG0baaaiaawUhaaaaa@6155@
n
= 1, 2, 3, …
9. Skriv in tal i området A1:A10. Lägg sedan in formeln =A2-A1 i cell B2 samt kopiera till
området B2:B10. Skriv sedan in formeln =SUMMA(B2:B10)
i exempelvis cell D2. och Formeln =A10-A1
i cell E2
Variera nu
innehållet i området A1:A10. Förklara resultatet.
10. Man kan bevisa att nedanstående former gäller
a)
∑
k=1
n
k
2
=
2
n
3
+3
n
2
+n
6
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaabCaeaacaWGRbWaaWbaaSqabeaacaaIYaaaaaqaaiaadUgacqGH9aqpcaaIXaaabaGaamOBaaqdcqGHris5aOGaeyypa0ZaaSaaaeaacaaIYaGaamOBamaaCaaaleqabaGaaG4maaaakiabgUcaRiaaiodacaWGUbWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamOBaaqaaiaaiAdaaaaaaa@4775@
b)
∑
k=1
n
k
3
=
n
2
(n+1)
4
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaabCaeaacaWGRbWaaWbaaSqabeaacaaIZaaaaaqaaiaadUgacqGH9aqpcaaIXaaabaGaamOBaaqdcqGHris5aOGaeyypa0ZaaSaaaeaacaWGUbWaaWbaaSqabeaacaaIYaaaaOGaaiikaiaad6gacqGHRaWkcaaIXaGaaiykaaqaaiaaisdaaaaaaa@4546@
Visa i ett
kalkylblad numeriskt att formlerna gäller för n =
1, 2, .... 20.
Om du vill
bevisa formlerna kan du göra så här. Vi tar itu med
∑
k=1
n
k
2
=
2
n
3
+3
n
2
+n
6
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaabCaeaacaWGRbWaaWbaaSqabeaacaaIYaaaaaqaaiaadUgacqGH9aqpcaaIXaaabaGaamOBaaqdcqGHris5aOGaeyypa0ZaaSaaaeaacaaIYaGaamOBamaaCaaaleqabaGaaG4maaaakiabgUcaRiaaiodacaWGUbWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamOBaaqaaiaaiAdaaaaaaa@4775@
.
Sätt
S
n
=
2
n
3
+3
n
2
+n
6
.
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaakiabg2da9maalaaabaGaaGOmaiaad6gadaahaaWcbeqaaiaaiodaaaGccqGHRaWkcaaIZaGaamOBamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaad6gaaeaacaaI2aaaaiaac6caaaa@426A@
Visa att
S
k
−
S
k−1
=
k
2
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGRbaabeaakiabgkHiTiaadofadaWgaaWcbaGaam4AaiabgkHiTiaaigdaaeqaaOGaeyypa0Jaam4AamaaCaaaleqabaGaaGOmaaaaaaa@3F65@
samt att
S
n
=
∑
k=1
n
(
S
k
−
S
k−1
)
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaakiabg2da9maaqahabaWaaeWaaeaacaWGtbWaaSbaaSqaaiaadUgaaeqaaOGaeyOeI0Iaam4uamaaBaaaleaacaWGRbGaeyOeI0IaaGymaaqabaaakiaawIcacaGLPaaaaSqaaiaadUgacqGH9aqpcaaIXaaabaGaamOBaaqdcqGHris5aaaa@46FC@
.
Vi har nu att
∑
k=1
n
k
2
=
∑
k=1
n
(
S
k
−
S
k−1
)=
S
n
=
2
n
3
+3
n
2
+n
6
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaabCaeaacaWGRbWaaWbaaSqabeaacaaIYaaaaaqaaiaadUgacqGH9aqpcaaIXaaabaGaamOBaaqdcqGHris5aOGaeyypa0ZaaabCaeaadaqadaqaaiaadofadaWgaaWcbaGaam4AaaqabaGccqGHsislcaWGtbWaaSbaaSqaaiaadUgacqGHsislcaaIXaaabeaaaOGaayjkaiaawMcaaiabg2da9iaadofadaWgaaWcbaGaamOBaaqabaGccqGH9aqpaSqaaiaadUgacqGH9aqpcaaIXaaabaGaamOBaaqdcqGHris5aOWaaSaaaeaacaaIYaGaamOBamaaCaaaleqabaGaaG4maaaakiabgUcaRiaaiodacaWGUbWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamOBaaqaaiaaiAdaaaaaaa@599C@
.
Du kan nu genomföra
beviset av formeln i b) på motsvarande sätt.
11. Geometriska talföljder
En talföljd
a
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaaaaa@37E9@
, n = 1,
2, 3 … kallas geometrisk om kvoten mellan ett tal och det föregående alltid har
samma värde, k. Det betyder att
a
k
a
k−1
=k
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWGHbWaaSbaaSqaaiaadUgaaeqaaaGcbaGaamyyamaaBaaaleaacaWGRbGaeyOeI0IaaGymaaqabaaaaOGaeyypa0Jaam4Aaaaa@3DAA@
, k = 2, 3, 4 … (1)
k
kallas den geometriska talföljdens kvot.
Om den första termen
a
1
=a
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaaIXaaabeaakiabg2da9iaadggaaaa@39A7@
får vi att
a
2
=ak
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaaIYaaabeaakiabg2da9iaadggacaWGRbaaaa@3A98@
,
a
3
=a
k
2
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaaIZaaabeaakiabg2da9iaadggacaWGRbWaaWbaaSqabeaacaaIYaaaaaaa@3B82@
,
a
4
=a
k
3
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaaI0aaabeaakiabg2da9iaadggacaWGRbWaaWbaaSqabeaacaaIZaaaaaaa@3B84@
....
a
n
=a
k
n−1
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaakiabg2da9iaadggacaWGRbWaaWbaaSqabeaacaWGUbGaeyOeI0IaaGymaaaaaaa@3D97@
Låt
S
n
=
a
1
+
a
2
+ ... +
a
n
=
∑
i=1
n
a
i
=
∑
i=1
n
a
k
i−1
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaakiabg2da9iaadggadaWgaaWcbaGaaGymaaqabaGccqGHRaWkcaWGHbWaaSbaaSqaaiaaikdaaeqaaOGaey4kaSIaaGjbVlaaysW7caGGUaGaaiOlaiaac6cacaaMe8UaaGjbVlabgUcaRiaadggadaWgaaWcbaGaamOBaaqabaGccqGH9aqpdaaeWbqaaiaadggadaWgaaWcbaGaamyAaaqabaaabaGaamyAaiabg2da9iaaigdaaeaacaWGUbaaniabggHiLdGccqGH9aqpdaaeWbqaaiaadggacaWGRbWaaWbaaSqabeaacaWGPbGaeyOeI0IaaGymaaaaaeaacaWGPbGaeyypa0JaaGymaaqaaiaad6gaa0GaeyyeIuoaaaa@5DFA@
vara summan av n
första termerna i den geometriska talföljden
a
n
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaWGUbaabeaaaaa@37E9@
. Följande formel är välkänd.
S
n
=a
1−
k
n
1−k
, k≠1
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaakiabg2da9iaadggadaWcaaqaaiaaigdacqGHsislcaWGRbWaaWbaaSqabeaacaWGUbaaaaGcbaGaaGymaiabgkHiTiaadUgaaaGaaiilaiaaysW7caWGRbGaeyiyIKRaaGymaaaa@45EA@
(4)
Om k = 1 är
S
n
=na
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaakiabg2da9iaad6gacaWGHbaaaa@3AC4@
.
Gör ett kalkylblad med vilket du kan generera de
10 första termerna I en geometrisk talföljd med given första term och given kvot
samt bekräfta att formeln
S
n
=a
1−
k
n
1−k
, k≠1
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaakiabg2da9iaadggadaWcaaqaaiaaigdacqGHsislcaWGRbWaaWbaaSqabeaacaWGUbaaaaGcbaGaaGymaiabgkHiTiaadUgaaaGaaiilaiaaysW7caWGRbGaeyiyIKRaaGymaaaa@45EA@
gäller
för n = 1, 2, 3 ..... 10.
Om du inte vill kunna
behandla även fallet k = 1, kan du
använda OM - funktionen. Uttrycket =OM(k=1,
n*a, n*(1-k^n)/(1-k)) betyder
OM
k=1
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4Aaiabg2da9iaaigdaaaa@3895@
så är
S
n
=na
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaakiabg2da9iaad6gacaWGHbaaaa@3AC4@
annars
S
n
=a
1−
k
n
1−k
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaBaaaleaacaWGUbaabeaakiabg2da9iaadggadaWcaaqaaiaaigdacqGHsislcaWGRbWaaWbaaSqabeaacaWGUbaaaaGcbaGaaGymaiabgkHiTiaadUgaaaaaaa@403B@
´.
12. Division med rest. Euklides algoritm.
Om vi
dividerar 13 med 5 får vi kvoten 2
och resten 3 dvs
13=2⋅5+3
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGymaiaaiodacqGH9aqpcaaIYaGaeyyXICTaaGynaiabgUcaRiaaiodaaaa@3DC7@
.
Låt a och b vara heltal. Vi dividerar a
med b. Vi får kvoten
k
0
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4AamaaBaaaleaacaaIWaaabeaaaaa@37BB@
och resten
r
0
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBaaaleaacaaIWaaabeaaaaa@37C2@
.
Det betyder att
a = k0b + r0 , 0 £ r0 < b
Vi dividerar sedan b med
r
0
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBaaaleaacaaIWaaabeaaaaa@37C2@
.
Vi får kvoten resten
k
1
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4AamaaBaaaleaacaaIXaaabeaaaaa@37BC@
0ch resten
r
1
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBaaaleaacaaIXaaabeaaaaa@37C3@
.
Det betyder att
b = k1r0 + r1 0 £ r1 < r0
r0 = k2r1 + r2
0 £ r2 < r1
⋮
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeSO7I0eaaa@37D2@
rn-2 = knrn-1 + rn 0 £ rn < rn-1
rn-1 = kn+1rn
Vi ser att vi får en
strängt avtagande följd av rester. Det måste därför finnas en sista positiv
rest
r
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBaaaleaacaWGUbaabeaaaaa@37FB@
.
r
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBaaaleaacaWGUbaabeaaaaa@37FB@
kallas den sista icke försvinnande resten i
Euklides algoritm. Ovanstående metod att med succesiva divisioner med rest
bestämma
r
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBaaaleaacaWGUbaabeaaaaa@37FB@
kallas Euklides algoritm. Man kan bevisa att
r
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBaaaleaacaWGUbaabeaaaaa@37FB@
är den största gemensamma delaren (faktorn)
till a och b.
Skapa ett kalkylark med vilket du kan bestämma
kvoter och rester i Euklides algoritm.
Det finns en
kalkybladsfunktion, HELTAL(x) som ger
det största heltalet, som är mindre än x.
Exempelvis är HELTAL(13/5) = 2.
Om man
dividerar a med b ges kvoten av k = HELTAL(a/b) och resten r = a
- kb. Man kan även använda kalkylbladsfunktionen REST(x;y) som ger resten vid
divisvion av x med y. Exempelvis är REST(13;5)=3.
Bestäm största gemensamma delaren till
a) 36 och
48 Resultat: 12
b) 56088 och 36777 Resultat: 123
c) 1591659,
1244961 och 583083. Resultat: 15759
d) Bevisa att
r
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBaaaleaacaWGUbaabeaaaaa@37FB@
är den största gemensamma delaren (faktorn)
till a och b.
Ledning: Visa
att varje tal, som delar a och b delar
r
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBaaaleaacaWGUbaabeaaaaa@37FB@
samt att
r
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOCamaaBaaaleaacaWGUbaabeaaaaa@37FB@
delar a
och b.
13.
Beräkna de 30 första talen i talföljden given genom
a)
{
x
1
=0,2
x
n+1
=3−14
x
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabeqaaiaadIhadaWgaaWcbaGaaGymaaqabaGccqGH9aqpcaaIWaGaaiilaiaaikdaaeaacaWG4bWaaSbaaSqaaiaad6gacqGHRaWkcaaIXaaabeaakiabg2da9iaaiodacqGHsislcaaIXaGaaGinaiaadIhadaWgaaWcbaGaamOBaaqabaaaaOGaay5Eaaaaaa@4632@
b)
{
x
1
=0,25
x
n+1
=3,25−12
x
n
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaiqaaqaabeqaaiaadIhadaWgaaWcbaGaaGymaaqabaGccqGH9aqpcaaIWaGaaiilaiaaikdacaaI1aaabaGaamiEamaaBaaaleaacaWGUbGaey4kaSIaaGymaaqabaGccqGH9aqpcaaIZaGaaiilaiaaikdacaaI1aGaeyOeI0IaaGymaiaaikdacaWG4bWaaSbaaSqaaiaad6gaaeqaaaaakiaawUhaaaaa@491A@
Är resultatet korrekt?
Svar och anvisningar
1. Skriv in ett jämnt tal i cell A1 samt formeln =2+A1 i cell A2. Använd kommandot Redigera Fyll ned.
2. Skriv in ett udda tal i cell B1 samt
formeln =2+B1 i cell C1. Använd kommandot
Redigera Fyll höger.
3. Skriv in 0
och 1 i cellerna A1 resp. A2 samt formeln =A1+A2 i cell A3. Använd kommandot Redigera Fyll ned. Skriv in formeln =A53 i cell B1. Då blir det bekvämare att avläsa värdet på a53 när man ändrar värdena på a1 och a2.
Resultat: a1 = 0 och a2 = 1 ger a53 = 32951280099.
a1 = 1 och a2 = 1 ger a53 = 53316291173. (Använd kommandot Format Kolumn Bredd….) för att ge
kolumnen en lämplig bredd.
4. Räntesats: 7
0 1000 15000 25000 30000
5 1402,55 21038,28 35063,79 42076,55
10 1967,15 29507,27 49178,78 59014,54
15 2759,03 41385,47 68975,79 82770,95
20 3869,68 58045,27 96742,11 116090,53
5. Man kan beräkna den förändringsfaktor, som gäller
för varje år samt sedan använda att behållningen i början av ett år är
behållningen ett år tidigare multiplicerat med den tillväxtfaktor, som gällt
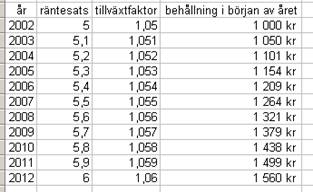
under det gångna året.
I a) får vi detta
resultat.
7. Beräkna
f(a + h) - f(a)
h
MathType@MTEF@5@5@+=feaagCart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8sipiYdHaVhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWcaaqaaiaadAgacaWGOaGaamyyaiaadccacaWGRaGaamiiaiaadIgacaWGPaGaamiiaiaad2cacaWGGaGaamOzaiaadIcacaWGHbGaamykaaqaaiaadIgaaaaaaa@40D3@
för
h = 1, 0,1, 0,001, ...
0,000000001
h (exp(a+h)‑exp(a))/h a
1 =(EXP($C$2+A2)‑EXP($C$2))/A2 1
=A2/10 =(EXP($C$2+A3)‑EXP($C$2))/A3
=A3/10 =(EXP($C$2+A4)‑EXP($C$2))/A4
=A4/10 =(EXP($C$2+A5)‑EXP($C$2))/A5
=A5/10 =(EXP($C$2+A6)‑EXP($C$2))/A6
=A6/10 =(EXP($C$2+A7)‑EXP($C$2))/A7
=A7/10 =(EXP($C$2+A8)‑EXP($C$2))/A8
=A8/10 =(EXP($C$2+A9)‑EXP($C$2))/A9
=A9/10 =(EXP($C$2+A10)‑EXP($C$2))/A10
=A10/10 =(EXP($C$2+A11)‑EXP($C$2))/A11
h (exp(x+h)‑exp(x))/h x
1 4,67077427 1
0,1 2,858841955
0,01 2,731918656
0,001 2,719641423
0,0001 2,718417747
0,00001 2,71829542
0,000001 2,718283187
0,0000001 2,718281964
0,00000001 2,718281777
0,000000001 2,718282044
8. a) Lägg in talen 1, 2,
3, 4 …. i A1, A2, A3, A4,….
b) Lägg in formeln =2*A1 i cell B1 samt formeln =3*A2 i cell B2.
c) Markera området B1 :
B2.
d) Utför kopiering nedåt
med hjälp av musen på samma sätt, som det som beskrivs i Exempel 3.
De 10 första
talen i den sökta talföljden är 2, 6, 6, 12, 10, 18, 14, 24, 18, 30.
Man kan alltså kopiera
formler, som är olika och som ligger under varandrara, nedåt.
9. Cellerna D2 och E2 har alltid samma innehåll. Detta kan
förklaras så här. Om man har 10 tal,
a
1
,
a
2
,
a
3
…
a
10
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaaIXaaabeaakiaacYcacaaMe8UaamyyamaaBaaaleaacaaIYaaabeaakiaacYcacaaMe8UaamyyamaaBaaaleaacaaIZaaabeaakiablAciljaaysW7caWGHbWaaSbaaSqaaiaaigdacaaIWaaabeaaaaa@452D@
och bildar
(
a
2
−
a
1
)+(
a
3
−
a
2
)+(
a
4
−
a
3
)+…+(
a
10
−
a
9
)
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacaWGHbWaaSbaaSqaaiaaikdaaeqaaOGaeyOeI0IaamyyamaaBaaaleaacaaIXaaabeaaaOGaayjkaiaawMcaaiabgUcaRmaabmaabaGaamyyamaaBaaaleaacaaIZaaabeaakiabgkHiTiaadggadaWgaaWcbaGaaGOmaaqabaaakiaawIcacaGLPaaacqGHRaWkdaqadaqaaiaadggadaWgaaWcbaGaaGinaaqabaGccqGHsislcaWGHbWaaSbaaSqaaiaaiodaaeqaaaGccaGLOaGaayzkaaGaey4kaSIaeSOjGSKaey4kaSYaaeWaaeaacaWGHbWaaSbaaSqaaiaaigdacaaIWaaabeaakiabgkHiTiaadggadaWgaaWcbaGaaGyoaaqabaaakiaawIcacaGLPaaaaaa@53FA@
får man resultatet
a
10
−
a
1
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyyamaaBaaaleaacaaIXaGaaGimaaqabaGccqGHsislcaWGHbWaaSbaaSqaaiaaigdaaeqaaaaa@3B40@
Allmänt
gäller
∑
k=1
n
(
a
k+1
−
a
k
)=
a
n+1
−
a
1
MathType@MTEF@5@5@+=feaagCart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaabCaeaadaqadaqaaiaadggadaWgaaWcbaGaam4AaiabgUcaRiaaigdaaeqaaOGaeyOeI0IaamyyamaaBaaaleaacaWGRbaabeaaaOGaayjkaiaawMcaaiabg2da9iaadggadaWgaaWcbaGaamOBaiabgUcaRiaaigdaaeqaaOGaeyOeI0IaamyyamaaBaaaleaacaaIXaaabeaaaeaacaWGRbGaeyypa0JaaGymaaqaaiaad6gaa0GaeyyeIuoaaaa@4B67@
,
ett resultat som är mycket användbart i många sammanhang.
12. a) 12 b)
123 c) 15759



![]() . Man kan minska antalet decimaler med ikonen Minska decimal,
. Man kan minska antalet decimaler med ikonen Minska decimal, ![]() .
. 

