Kvadreringsregeln
Denna sida innehåller en mycket ingående genomgång av och förklaring till kvadreringsregeln.
Vi skall undersöka skillnaden mellan att å ena sidan först addera två tal och sedan kvadrera resultatet och å andra sidan att först kvadrera de två talen och sedan addera resultatet. Vi skall se att denna skillnad är talens dubbla produkt. Detta kan enkelt uttryckas med en matematisk formel,
(a + b)2 - (a2 + b2) = 2ab.
Denna formel kallas kvadreringsregeln och brukar oftast skrivas så här:
(a + b)2 = a2 + b2+ 2ab
Kvadrera
Att kvadrera ett tal innebär att multiplicera talet med sig självt. Resultatet kallas talet i kvadrat.
Exempelvis är 5 i kvadrat 25. Man skriver: 52 = 25.
Kommentar
Man kan bekymra sig för varför man använder orden kvadrat och kvadrera på detta sätt. När man ägnar sig åt matematik måste man, liksom i många andra sammanhang, vara beredd på att ord kan ha helt olika betydelse i olika sammanhang. Ordet kvadrat betyder som bekant även en rätvinklig liksidig fyrhörning. När man säger 5 i kvadrat skulle det kunna betyda att man har placerat en femma i en kvadrat. Man måste förstå vad orden, som används i matematiken, betyder i just det sammanhang som är aktuellt. Annars kan man naturligtvis inte förstå. Om man förstår vad orden betyder kan vara nöjd. Man bör inte låta det bli ett problem varför orden betyder det de betyder. Detta kan visserligen vara intressant och berikande att fundera på, men man bör ägna måttligt med tid på detta.
Att addera två tal är samma sak som att lägga ihop dem eller att ”plussa” talen. Resultatet av en addition kallas summa.
Att kvadrera en summa och addera kvaderade tal
a. Tänk dig att du först adderar två tal och att du sedan kvadrerar resultatet.
Om de två talen är 5 och 7, får man om man först adderar, 5 + 7 = 12. Efter kvadrering får vi (5 + 7)2 = 122= 144.
b. Tänk dig sedan att du gör det du gjorde i a. men i omvänd ordning. D.v.s. du börjar med att kvadrera de två talen och att du sedan adderar resultaten.
Vi får 52 = 25 och 72 = 49. Efter addition får man 52 + 72 = 25 + 49 = 74
Kommentar
Det blir i detta i detta fall olika resultat om man adderar först och kvadrerar sedan jämfört med om man först kvadrerar och sedan adderar. Detta är ganska normalt. I allmänhet är det i livet stor skillnad om man gör saker i olika ordning. Det är exempelvis stor skillnad på att först ta på sig en socka och sedan en sko mot att först ta på sig skon och sedan sockan.
Skillnaden mellan att först addera och sedan kvadrera och att först kvadrera och sedan addera är i vårt fall (5 + 7)2 - (52 + 72) = 144 - 74 = 70.
Vi gör samma sak med talen 3 och 4. Vi får (3 + 4)2 - (32 + 42) = 49 - (9 + 16) = 49 - 25 = 24.
Även i detta fall ser vi att man får olika resultat om man först adderar och sedan kvadrerar mot att först kvadrera och sedan addera.
Viktig slutsats
(a + b)2 = a2 + b2gäller inte för alla värden på a och b. (Åtminstone inte om a = 5 och b = 7 samt om a = 3 och b = 4Vi skall nu undersöka hur stor skillnaden är mellan uttrycken (a + b)2 och a2 + b2). Vi tittar på två exempel.
Exempel 1. Geometriskt bevis av kvadreringsregeln
Vi tänker oss nu en kvadrat med sidan. Vi delar in sidorna i två delar enligt figuren nedan.
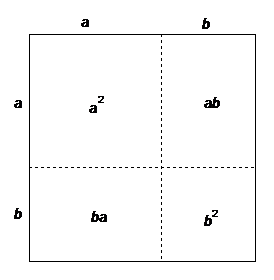
Eftersom arean av hela kvadraten är lika med summan av de fyra delareorna inser man att
(a + b)2 = a2 + b2+ ab + ba = a2 + b2+ 2ab
Vi ser att skillnaden mellan (a + b)2 och a2 + b2 är 2ab.
Eftersom a och b kan vara vilka positiva tal som helst har vi åstadkommit ett geometriskt bevis för att
(a + b)2 = a2 + b2+ 2ab
för alla positiva värden på a och b.Jag kan nu glädja läsaren med att det förhåller sig så att om en likhet av ovanstående typ gäller för alla positiva värden på a och b, så gäller den för alla värden på a och b. Detta kan man bevisa.
Påståendet att
(a + b)2 = a2 + b2+ 2ab
gäller för alla värden på a och b, kallas kvadreringsregeln. Ibland kallas denna regel för första kvadreringsregeln.
Man kan uttrycka kvadreringsregeln i ord på vanlig svenska t.ex. så här:
Att kvadrera summan av två tal ger alltid samma resultat som att bilda summan dessa tals kvadrater och talens dubbla produkt. (2ab är ju en fördubbling av ab, som är en produkt.)
Vi skall nu titta på ett annat exempel
Exempel 2. Bevis av kvadreringsregeln med karameller
En gammal kvinna tyckte mycket om att ge barn, som besökte henne, karameller. Ju fler karameller hon fick tillfälle att dela ut desto trevligare tyckte hon att det var. Därför gjorde hon så att hon gav varje besökande barn lika många karameller som antalet besökande barn.
En dag besöktes hon av a pojkar. Dessa fick då sammanlagt a2 karameller. Senare samma dag besöktes hon av b flickor. Dessa fick sammanlagt b2 karameller. Denna dag hade hon alltså delat ut totalt a2 + b2 karameller.
Nästa dag bestämde sig pojkarna och flickorna att besöka kvinnan samtidigt. De hade tänkt ut att i så fall skulle de ju få a + b karameller var. Totalt fick kvinnan dela ut (a + b)2 karameller den andra dagen. Barnen var mycket intresserade av algebra. De förstod att de var och en fått fler karameller än dagen före. De funderade därför på hur många fler karameller kvinnan totalt hade delat ut än hon gjort dagen innan. De enades om att varje pojke fått b karameller mer p.g.a. att flickorna var med. Pojkarna fick därför sammanlagt ab fler karameller. De insåg sedan på samma sätt att flickorna fått sammanlagt ba fler karameller än dagen innan. De förstod att den gamla kvinnan delat ut ab + ba = 2ab fler karameller.
Barnen blev alla mycket glada att de kunde dra slutsatsen att antalet karameller kvinnan delat ut andra dagen, var det hon delat ut första dagen, a2+b2, plus det som hon delat ut mer andra dagen, 2ab.
Ett av barnen sade då glädjestrålande då måste ju (a + b)2 = a2 + b2+ 2ab. Det var ju detta vår matematiklärare försökte lära oss idag och som han kallade kvadreringsregeln! (Fritt efter Gelfand - Shen, Algebra)
I detta exempel är a och b positiva heltal, vilka som helst. Exempel 2 visar oss att (a + b)2 = a2 + b2+ 2ab för alla positiva heltal a och b.
Nu är det så att man kan bevisa att, om en likhet av typen (a + b)2 = a2 + b2+ 2ab gäller för alla positiva heltalsvärden på a och b, så gäller den för alla värden på a och b.
Bevis av kvadreringsregeln
Det enda man behöver göra är att utföra multiplikationen (a + b)(a + b) och övertyga sig om att resultatet gäller för alla värden på a och b.
Man kan göra så här:
\({{\left( a+b \right)}^{2}}=\underbrace{\left( a+b \right)}_{=c}\cdot \left( a+b \right)\)\(=c\cdot \left( a+b \right)=c\cdot a+c\cdot b=\)\(\left( a+b \right)\cdot a+\left( a+b \right)\cdot b=\)\({{a}^{2}}+b\cdot a+a\cdot b+{{b}^{2}}={{a}^{2}}+2a\cdot b+{{b}^{2}}\)
Exempel på användning av kavdreringsregeln
1. Vi skall utveckla (2x + 3y)2 med kvadreringsregeln.
\[{{\left( \underbrace{2x}_{=a}+\underbrace{3y}_{=b} \right)}^{2}}={{\left( a+b \right)}^{2}}={{\underbrace{a}_{=2x}}^{2}}+2\underbrace{a}_{=2x}\underbrace{b}_{=3y}+{{\underbrace{b}_{=3y}}^{2}}=\]
\[{{\left( 2x \right)}^{2}}+{{\left( 3y \right)}^{2}}+2\cdot 2x\cdot 3y=4{{x}^{2}}+9{{y}^{2}}+12xy\]
Det är viktigt att förstå att kvadraten på 2x och 3y är 4x2 respektive 9y2, skilj alltså mellan (2x)2 = 4x2 och 2x2 samt mellan (3y)2 = 9y2 och 3y2
2. Vi skall undersöka (a - b)2
Om man kan teckenreglerna för räkning med reella tal kan man förstå följande att
a - b = a + (-b), 2a(-b) = -2ab och (-b)2 = b2
Vi får
(a - b)2 = (a + (-b))2 = a2 +(- b)2+ 2a(-b) = a2 + b2 +(- 2ab) =
a2 + b2- 2ab
(a - b)2 = a2 + b2- 2ab kallas andra kvadreringsregeln.